Negative Korrelation ist nicht immer erstrebenswert
Auf dem Weblog Der Privatanleger wurde die Frage diskutiert, ob eine negative Korrelation unbedingt erstrebenswert ist. Man hört ja immer wieder solche Dinge wie beispielsweise „Wertpapiere mit gegenläufiger Korrelation verringern das Gesamtrisiko des Portfolio“. Spätestens seit Harry Markowitz wissen wir, wie man durch Diversifikation das Risiko eines Portfolios mindern kann. Und wie wichtig dabei die sogenannten Korrelationen zwischen den Wertpapieren untereinander sind. Das ist eine Zahl zwischen -1 und +1.
Denn kombiniert man solche Wertpapiere, deren Korrelation nahe +1 ist, so ist der Diversifikationseffekt so gut wie Null. Eine gute, risikomindernde Diversifikation erhält man also nur dann, wenn solche Wertpapiere zusammenstellt, deren Korrelation echt kleiner als 1 ist. Also, so könnte man meinen, hat man die beste Diversifikation dann, wenn die Korrelation bei -1 liegt.
Ein klein wenig hat Der Privatanleger in diese Richtung argumentiert. Ich hingegen meine, dass eine Korrelation von zwischen -0,9 und -1,0 nicht erstrebenswert ist und man die besten Diversifikationseffekte bei einer Korrelation im Bereich -0,5 und +0,5 hat.
Der Privatanleger hat ein sehr gutes Beispiel für perfekt negativ korrelierte Wertpapiere A und B gebracht:
- Jahr 1: Rendite von A = +10%; Rendite von B = +5%
- Jahr 2: Rendite von A = +5%; Rendite von B = +10%
Tatsächlich handelt kann man hier die statistische Größe der Korrelation berechnen und erhält den Wert -1. Beide Wertpapiere haben eine erwartete Rendite von 7,5%.
Die Kombination von A und B hat dann auch erwarteten Rendite von 7,5% führt:
- Jahr 1: Mittelwert der Rendite von A und B= +7,5%
- Jahr 2: Mittelwert der Rendite von A und B= +7,5%
Und unter der Annahme, dass diese perfekte Gegenläufigkeit auch in der Zukunft so weitergeht, hätte man mit einem Portfolio, das aus A und B besteht, durchgängig eine Rendite von 7,5%. Wobei das Risiko bei Null liegt. Das Risiko wurde in diesem Beispiel also vollständig wegdiversifiziert. Denn wenn die beiden Wertpapiere perfekt gegenläufig sind, dann überschreitet das eine Wertpapier den Mittelwert von 7,5% immer in dem Maße, wie er von dem anderen Wertpapier unterschritten wird.
So weit, so gut. Es handelt sich hier ja um ein theoretisch-konstruiertes Beispiel. Die Frage ist, ob so etwas auch in der Realtiät vorkommen kann.
Nehmen wir an, ein solches Paar von Wertpapieren würde tatsächlich existieren. Dann wäre jeder Anleger dumm, wenn er nicht hälftig in genau diese beiden Wertpapiere investieren würde. Denn so kann jeder Anleger mit 100%iger Gewissheit und ohne jegliches Risiko eine Rendite von 7,5% erzielen.
Würde sich das tatsächlich herumsprechen, dann gäbe es einen solchen Ansturm auf diese beiden Wertpapiere, dass sich natürlich auch die zu erwartende Rendite mindern würde. Da es sich um einen risikofrei erzielbaren Ertrag handelt, müsste die zu erwartende Rendite letztlich auf Tagesgeldniveau sinken. Das ist das in der Ökonomie weitverbreitete Arbitrage-Argument.
Meine Schlussfolgerung aus dem Gesagten ist, dass – genau wegen dieses Arbitrage-Arguments – es sehr erstaunlich wäre, wenn man in der Realität zwei perfekt negativ korrelierte Wertpapiere finden könnte, deren Kombination eine Rendite erwarten ließe, die deutlich über Tagesgeld liegt.
Dennoch, wie gesagt, bewerben manche Anbieter sogenannte short-Produkte mit dem Argument, dass eine Beimischung das Gesamtportfolio risikoärmer machen würde. Und zwar wird gerade eine Korrelation bei nahe -1 als Garant für eine solch angeblich hervorragende Diversifikation genannt.
Ich habe es letztes Jahr auch immer wieder erlebt, dass mir Anleger Depots vorgelegt haben, bei denen beispielsweise ein Aktien-Depot mit einem short-DAX-ETF kombiniert wurde. In den Gesprächen glaubten diese Anleger, damit sehr klug gehandelt zu haben. Weil sie ja mit einer gegenläufigen Position ihr Wertpapier optimal diversifiziert hätte – wie sie meinten.
Tatsächlich war eine solche Beimischung von short-Produkten fast immer nicht sinnvoll. Denn die Kombination macht zwar das Gesamtprotfolio risikoärmer. Das ist richtig. Die zu erwartende Rendite sinkt aber auch entsprechend, manchmal sogar unter Tagesgeld-Niveau. Und in diesem Falle wäre es dann sinnvoller, lieber Aktienpositionen zu verkaufen und direkt in Tagesgeld anzulegen, als solche Aktienpositionen mit einem short-Produkt zu kombinieren.
Hier ein konkretes Beispiel. Ich habe mir mal ein short-DAX-ETF (DBX1DS) angesehen im Verhältnis zu einem DAX-ETF (DBX1DA) angesehen. Und zwar über den Zetiraum von 4.1.2010 bis 2.03.2011 auf Tagesbasis.
Die Korrelation habe ich für diesen Zeitraum berechnet: -0,997. Also fast bei -1.
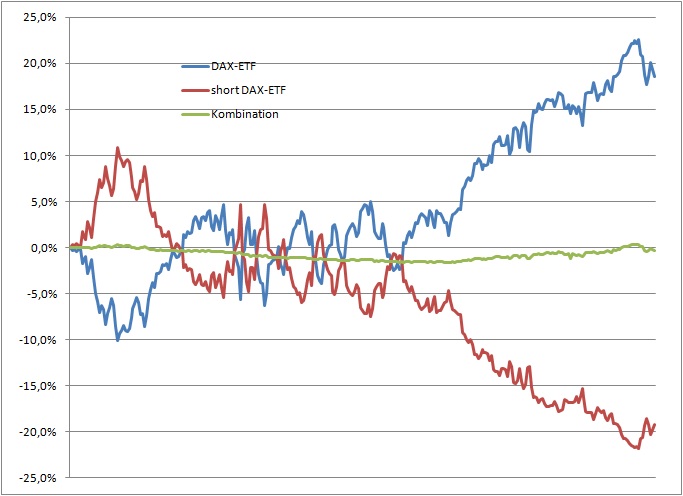
Nehen wir nun einen Anleger an, der Anfang Januar 2010 einen Betrag von 50.000 Euro in den DAX-ETF und 50.000 Euro in den short-DAX-ETF angelegt hat. Dann ergibt sich folgender Chart:
Man sieht hier sehr schön: Wenn der DAX-ETF steigt, fällt entsprechen der short-DAX-ETF. Und umgekehrt. Direkt spiegelbildlich. Die Verluste des einen Wertpapieres werden also umgehend durch Gewinne des anderen ausgeglichen. Eine perfekte negative Korrelation.
Nur: Was hat der Anleger am Ende davon?
Der wird am Ende dieser Periode keine 100.000 Euro mehr haben, sondern nur noch 99.683,64 Euro.
Diese vermeintlich perfekte Diversifikation hat dem Anleger also zwar große Sicherheit gebracht, aber mit dem Ergebnis, keine Rendite erzielt zu haben. In diesem Falle sogar unterhalb der Tagesgeldrendite.
Daher mein Rat an alle, die über short-Produkte nachdenken: Eine negative Korrelation in der Nähe von -1 ist fast nie sinnvoll. Ich möchte zwar nicht ausschließen, dass so ein Fall auftregen kann. Aber wegen des Arbitrage-Argument, wäre es sehr erstaunlich, zwei perfekt negativ korrelierte Wertpapiere zu finden, deren Kombination eine Rendite von deutlich über Tagesgeld erwarten lässt.
Wenn man sein Portfolio optimal diversifizieren möchte, sollte man darauf achten, solche Anlageklassen zu kombinieren, deren Korrelation sich nach Möglichkeit zwischen -0,5 und +0,5 bewegt. Hier erhält man die besten Diversifikationseffekte, ohne dass gleich die Rendite in Mitleidenschaft gerät. Und bevor man sich ein short-Produkt ins Depot legt, sollte man darüber nachdenken, dass der Verkauf von Aktien zugunsten von Tagesgeld nicht vielleicht die bessere Alternative ist.

Danke, dass Sie das Thema hier noch einmal aufgreifen.
Ich glaube, was die wesentlichen praxisrelevanten Punkte angeht, sind wir uns recht einig:
– Der Versuch, mittels eines Long- und eines Short-ETF auf den gleichen Index die Schwankungen des eigenen Portfolios zu minimieren, ist einigermaßen schwachsinnig.
– Will man nicht eine derartige Long-Short-Strategie fahren, ist es sehr schwer bis unmöglich (mir zumindest fällt keine Möglichkeit ein), so stark negativ korrelierte Assets zu finden.
Dennoch ist – ceteris paribus – immer eine möglichst stark negative Korrelation anzustreben, wenn man den Diversifikationseffekt in einem Portfolio aus zwei Assets minimieren will. Die von Ihnen angegebene Spanne von 0,5 bis -0,5 halte ich für willkürlich (aber sie soll ja auch eher Anhaltspunkte für eine vernünftige Anlagestrategie liefern – und das tut sie sicher).
Die Gründe dafür, dass es nicht genügt, sich bei einer derartigen Betrachtung nur auf die Korrelation zu konzentrieren, hatte ich im Beitrag auf Der Privatanleger bzw. der Diskussion dazu, ja schon einmal genannt: Ein vollkommen risikofreies Portfolio aus riskanten Einzel-Assets kann man nur dann zusammenstellen, wenn neben der zukünftigen Korrelation auch die zukünftige Volatilität und der Erwartungswert der Rendite bekannt sind. Das ist aber in der Realität unmöglich.
In meinem Beispiel dagegen ist das der Fall. Ich betrachte das inzwischen auch als Schwäche des Beispiels. Es ist aus diesem Grund zwar sehr überzeugend. Allerdings verleitet es auch zu dem Fehlschluss, dass die Korrelation das Ein und Alles ist. Dem ist aber nicht so.
Viele Grüße
Holger Handstein
Sehr geehrter Herr Handstein. Sie schreiben:
„Dennoch ist – ceteris paribus – immer eine möglichst stark negative Korrelation anzustreben, wenn man den Diversifikationseffekt in einem Portfolio aus zwei Assets minimieren will. “
Genau an dieser Stelle dreht sich unsere Argumentation ständig im Kreise.
Die Frage ist: Glauben Sie an (weitestgehend) effiziente Märkte oder nicht?
Ich nehme an, Sie tun das. Denn wenn ich Sie recht verstehe, glauben Sie auch daran, dass man mit aktivem Management kaum erwarten kann, passives Management langfristig zu schlagen. die Überlegenheit des passiven Management kann aber nur sein, wenn man an (weitgehend) effiziente Märkte glaubt.
Und „effizient“ bedeutet: Jede Möglichkeit zur Arbitrage wird von den Marktteilnehmern schnellstmöglich wahrgenommen. Alleine die Exsitenz so viele Hedgefonds lässt es als kaum wahrscheinlich erscheinen, dass zwei Wertpapiere nachhaltig deutlich negativ korreliert sind (sagen wir zwischen -0,8 und -1,0) und die Kombination beider Wertpapiere lässt mit einer erwarteten Rendite von deutlich über Tagesgeld.
Wenn Sie daran glauben sollten, dass es prinzipiell solche Wertpapiere geben könnte, dann müssten Sie auch daran glauben, dass die Märkte über weite Phasen ineffizient sind. Beides zusammen, (a) der Glaube an effiziente Märkte und (b) die Annahme zweier sehr weitgehend negativ korrelierter Wertpapiere mit einer erwarteten Rendite über Tagesgeld, passen einfach nicht zusammen.
Daher ist auch die Maxime „Möglichst starke negative Korrelation!“ falsch. Sie mag bei konstruierten, theoretischen Beispielen richtig sein – unter der Aushebelung der Annahme effizienter Märkte. Es ist richtig, dass die Kombination zweier Wertpapiere, die eine Korrelation zwsichen -0,9 und -1,0 haben, zu einem deutlich risikoärmeren Portfolio führt – aber in der Praxis auf Kosten der Rendite. In der Realtität werden Wertpapiere, die stark negativ korreliert sind, eine zu erwartende Rendite um Tagesgeld oder geringer haben – sofern die Annahme effizienter Märkte stimmt.
Gerade wenn man unbedarften Privatanlegern die Maxime „Möglichst negative Korrelation!“ an die Hand gibt, dann kommt es zu massiven Fehlentscheidungen und unsinnig sturkturierten Portfolios (wie ich es in meiner Beratungspraxis leider immer wieder sehe).
Daher wäre es gut, diese Maxime zu streichen. Erstens weil sie nur stimmt wenn man auch eine geringere Zielrendite in Kauf nimmt, und zweitens weil sie in der Praxis für Verwirrung sorgt.
Besser ist die Maxime: „Strebe eine Korrelation von um die Null an!“ So kann man für eine gute Diversifikation sorgen, und das nicht auf Kosten der Rendite. Und es ist eine Maxime, die Privatanleger bei ihren Anlageentscheidungen gut und schnell umsetzen können.
Wer stattdessen immer wieder hört, man solle solche Wertpapiere kombinieren, die eine möglichst negative Korrelation haben, der wird dann eben auch einen DAX-ETF mit einem shor-DAX-ETF kombinieren und das für eine schlaue Idee halten. Also: Hören wir bitte auf, Privatanleger falsch zu informieren, sondern so, dass es für sie hilfreich ist. Bitte!
Hallo!
Die unterschiedlichen Sichtweisen sind klar; und das nicht erst seit dem hiesigen Beitrag.
Dennoch haben beide Aspekte Ihre Berechtigung:
Herr Dr. Handstein betont den THEORETISCHEN Gedanken, dass man – UNTER ANSONSTEN GLEICHEN BEDINGUNGEN – möglichst negativ korrelierende Anlagen miteinander kombinieren sollte.
Herr Dr. Peterreins betont den PRAKTISCHEN Aspekt, dass man perfekt negativ korrelierende Anlagen, die (in Kombination) mehr als den risikolosen Zins bieten, wohl nicht finden wird.
Unter Berücksichtigung dessen kann von einer Falschinformation der Privatanleger keine Rede sein.
Viele Grüße!
OK, Sie haben recht. Es gibt den theoretischen Aspekt und den praktischen Aspekt dieser Fragestellung. Aber selbst der theoretische Aspekt funktioniert nur, wenn man die Annahme effizienter Märkte ausklammert. Fast jedes mir bekannte finanztheoretische Modell trifft aber exakt diese Annahme. Ich glaube ja selbst nicht an alles, was die Finanztheoretiker sagen (wie man leicht meinen Weblog-Artikeln entnehmen kann). Aber an eine weitestgehende Effizienz der Kapitalmärkte glaube ich schon. Gerade Arbitrage-Möglichkeiten werden von Hedgefondsmanagern in der Regel sehr schnell erkannt und deswegen auch tendenziell beseitigt.
Das Problem ist aber, dass Herr Handstein seine Auffassung mit den negativen Korrelation nicht nur als theoretische These, sondern als praktische Handlungsmaxime formuliert. Ich zitiere noch einmal:
„Dennoch ist – ceteris paribus – immer eine möglichst stark negative Korrelation anzustreben, wenn man den Diversifikationseffekt in einem Portfolio aus zwei Assets minimieren will. “
Das ist der Wortlaut von Herrn Handstein. Er hält „möglichst stark negative Korrelationen“ für erstrebenswert. Ich sage: Nein, das ist definitiv nicht erstrebenswert. Und das zu behaupten, bedeutet, normale Privatanleger in die Irre zu führen.
Das Erebnis solcher verwirrender Informationen sind dann genau solche Portfolios, in denen ich neben einem DAX-ETF einen short-DAX-ETF finde – plus einem stolzen Anleger, der meint, er hätte optimal diversifizert. So ist halt nun mal die Praxis, wie ich sie seit etwa einem Jahr immer wieder erlebt habe. Ich halte es hier für extrem wichtig, die Anleger korrekt zu informieren und zu sagen: „Nein, eine möglichst hohe negative Korrelation ist nicht unbedingt erstrebenswert!“ – Das wäre eine gute und klare Information, die den normalen Privatanleger vor Fehlentscheidungen bewahren würde.
Die Behauptung „Eine möglichst hohe negative Korrelation ist erstrebenswert“ ist theoretisch nur dann richtig, wenn man nicht an effiziente Märkte glaubt. Und sie für praktisch zu unsinnig strukturierten Portfolios. Also verzichten wir doch bitte auf diese Behauptung. Nochmals und flehentlich: Bitte!
Vielleicht beleuchtet diese Diskussion noch etwas anderes. Ich höre immer wieder: „Man braucht eigentlich gar keinen Anlageberater. Das kann man alles auch selbst machen.“ Gerade diese Diskussion, inwiefern eine möglichst negative Korrelation erstrebenswert sei, zeigt mir sehr deutlich, dass eine professionelle, kompetente Anlageberatung sehr wichtig ist. Normale Privatanleger rennen immer wieder in teure Fallen. Und so ist auch die Maxime „Eine möglichst hohe negative Korrelation ist erstrebenswert!“ eine teure Falle, vor der ein guter Anlageberater bewahren kann.
Da gäbe es natürlich noch eine ganze Reihe von Beispielen. Aber das ist natürlich direkt exemplarisch, wie man als Anleger glaubt „gut informiert“ zu sein, und dennoch genau das Falsche macht -sogar basierend auf dieser „guten Information“, die man irgendwo augeschnappt hat und die man unbesehen glaubt. Schwupps hat man ein Depot, indem man neben einem DAX-ETF einen short-DAX-ETF hat. Hat man das nicht eben irgenwo gelesen, dass eine möglichst hohe negative Korrelation ein Depot gut diversifiziert?
Ich denke, es wäre besser gewesen, wenn ein solcher vermeintlich „gut informierter“ Anleger ein wenig Geld für ein Beratungshonorar in die Hand genommen hätte, um sich damit eine kompetente Anlageberatung zu holen. Das wäre für einen solchen Anleger günstiger, als in die DAX-ETF- plus short-DAX-ETF-Falle zu schlittern.
Lieber Herr Dr. Peterreins,
ich finde Ihre Argumentation zu diesem Thema durchaus nachvollziehbar. Ich bin mir nur unsicher, ob das Arbitrage-Argument hier wirklich so zieht, wie Sie es beschreiben. Es wird ja oft davon gesprochen, dass eine sinnvolle Diversifikation das einzige „free lunch“ bei Investments ist. Wenn man Ihrer Argumentation konsequent folgt, dann müssten die effizienten Märkte dieses „free lunch“ ja auch verschwinden lassen.
Ich bin auch skeptisch, weil ich noch nie irgendwo etwas in dieser Art gelesen habe. Mich wundert es, dass kein anderer (mir bekannter) Autor bzw. Wissenschaftler das bisher so klar benannt hat. Können Sie uns einen wissenschaftlichen Artikel oder ein Buch zu diesem Thema nennen, in dem wir uns dazu schlau machen können?
Beste Grüße,
Matthias Hofmann
Vielen Dank, sehr geehrter Herr Hormann, für Ihren Kommentar.
Den sog. free lunch durch optimale Diversifikation hat man durch Anlageformen, deren Korrelation so um die Null liegt. Sagen wir zwischen -0,5 und 0,5.
Nehmen wir das Beispiel einer perfekt negativen Korrelation. A und B sind zwei Wertpapiere, die perfekt negativ korreliert sind. Die Kombination beider Wertpapiere führt dazu, dass ihre gemeinsame zu erwartende Rendite mit 100%iger Sicherheit erreicht wird. 100%ig! Das ist der Punkt. Und wenn man eine Rendite mit absoluter Sicherheit erreichen kann, dann wäre jeder dumm, wenn er nicht genau diese beiden Wertpapiere kombinieren würde – es sei denn die gemeinsam zu erwartende Rendite liegt bei Tagesgeld oder sogar darunter.
Der „free lunch“, der bei otpimaler Diversifikation gemeint ist, ist nie, dass eine Rendite mit 100%iger Sicherheit zu erreichen ist. Sondern dass eine zu erwartende Rendite (die oberhalb der Tagesgeldrendite liegen sollte) mit möglichst wenig Risiko zu erreichen ist. Eins ist aber klar: Wenn die Zielrendite größer sein soll, als mit Tageslgeld erreichbar, dann muss ein gewisses Risiko dabei sein.
Sagen wir mal, die Zielrendite ist 5% p.a. Dann kann man Portfolios zusammenstellen, die diese Zielrendite haben, nur das eine Portfolio (A) hat eine zu erwartende Volatilität von 7% und das andere (B) eine Vola von 15%. Der „free lunch“ der Diversifikation besteht darin, das Portfolio mit dem geringeren zu erwartenden Risiko bei gleicher Zielrendite zu wählen. In diesem Fall ist also das Portfolio (A) zu wählen. Und sicherlich werden die Korrelationen des Portfolios (A) „besser“ sein als die von (B).
Wie gessagt: Der free-lunch kann nicht bedeuten, eine Zielrendite oberhalb von Tagesgeld absolut sicher zu erhalten. Das wäre eine Missverständnis. Und genau hier fängt der springende Punkt an. Kombiniert man zwei Wertpapiere mit einer Korrelation von -0,9 oder -1,0, dann hat man zwar das Risiko des Portfolios reduziert, aber eben auch die Zielrendite. Es kann sich also um keine Optimierung im Sinne von Markowitz handeln. Wenn man das Risiko gegen Null schiebt, steht auch bei Markowitz links unten: Tagesgeld (bzw. eben das risikolose Investment).
Optimierung besteht darin, bei gleichbleibender Zielrendite das Risiko zu minimieren. Oder umgekehrt: bei gleichbleibendem Risiko die Zielrendite möglichst zu maximieren. Eine von beiden Komponenten muss bei der Optimierung konstant gehalten werden. Das ist ein typisches Missverständnis von Markowitz, wenn man versucht beider Faktoren gleichzeitig zu „optimieren“. Das Ergebnis ist dann eben Tagesgeld. Aber das will man ja im allgemeinen nicht, man will ja eine höhere Zielrendite als mit Tagesgeld möglich ist. Und nicht etwa ein kompliziert zusammengestelltes Portfolio, das vom Ergebnis zwar Null Risiko hat, aber eben auch Null Überrendite zum Tagesgeld. Dann könnte man sich auch die komplizierte Zusammenstellung sparen.
Ich habe ja bisher sehr gute Erfahrungen gemacht mit dem MAN AHL-Trendfolgesystem. Kunden, die stark in Aktien-Investments engagiert sind und durch eine ganz andere Anlageklase für eine bessere Diversifikation sorgen wollen, rate ich zu diesem Hedgefonds. Die Korrelation zum Aktienmarkt dieses Trendfolgesystems von 1996 bis 2010 lag bei -0,18. Also ziemlich gut in dem von mir genannten Bereich -0,5 bis +0,5. Deswegen – weil hier die Korrelation in der Vergangenheit zwar negativ war, aber Nahe Null – deswegen handelt es sich hier um eine Anlageform, die gut diversifiziert.
Man könnte hier noch ergänzen. In dem abwärtsgehenden Markt von April 2000 bis März 2003 war die Korrelation des AHL-Trendfolgesystems zum Aktienmarktes -0,63. Ähnlich sah es in der jüngsten Abwärtsphase aus. In steigenden Märkten wie beispielsweise von April 2003 bis 2007 war die Korrelation dieser Strategie zum Aktienmarkt +0,4. Zu letzterem könnte man sagen: Gott sei Dank! Eine hohe negative Korrelation in steigenden wie fallenden Aktienmärkten ist ja gar nicht gut, denn das würde ja bedeutet, dass wenn die Aktienmärkte steigen, typischerweise die Hedgefonds-Strategie Geld verliert. Das will aber keiner.
Unter Strich liegt die Korrelation der AHL-Strategie bei einer „negativen Null“, und genau das ist erstrebenswert. Läge die Korrelation bei -0,9, dann müsste ich meinen Anlegern von dieser Hedgefonds-Strategie abraten mit dem Argument: „Ja, das Risiko wird hier wohl reduziert, sicher aber auch die zu erwartende Zielrendite Ihres Gesamtvermögens.“
Hallo Dr. Peterreins,
Ja, ich denke, dass Märkte weit gehend effizient sind. Aber ich habe auch schon mehrmals versucht, deutlich zu machen, dass negative Korrelation allein nicht ausreicht, um ein risikoloses Portfolio hinzubekommen – man muss eben auch die zukünftige Volatilität und den Erwartungswert der Rendite kennen. Man kennt aber keine der drei Größen, denn auch Korrelationen sind ja nicht konstant.
Und, wie Matthias Hofmann schreibt: Wenn man Ihre Argumentation konsequent zu Ende denkt, müssten alle möglichen Portfolios vor Kosten gleich effizient sein – weil jeglicher „Free Lunch“ sofort wegarbitriert würde. Das ist aber offenbar nicht der Fall.
Im Übrigen spricht auch die Existenz von Hedgefonds nicht unbedingt dafür, dass es keine Ineffizienzen gibt. Im Gegenteil: Wenn man davon ausgeht, dass Hedgefonds systematisch ein Alpha erzielen können, dann muss das an Markt-Ineffizienzen liegen, die ausgenutzt werden können. Wenn man überdies davon ausgeht, dass Hedgefonds sogar – nach zum größten Teil exorbitant hohen Kosten – eine systematische Überrendite für die Anleger erwirtschaften können, dann müssen diese Ineffizienzen sogar ziemlich groß sein.
All dies und die vielen – zum Beispiel durch Andrei Shleifer ausführlich und mit mehr Mathematik als ich verstehen kann – beschriebenen Gegebenheiten der realen Welt, die Arbitrage erschweren, lassen es für mich sehr unwahrscheinlich erscheinen, dass sich Diversifikationseffekte so leicht wegarbitrieren lassen.
Und die von Ihnen genannte Spanne von +0,5 bis -0,5 bleibt eben willkürlich. Warum nicht -0,6? Und warum soll ein KK von 0 das Optimum sein? Dafür fehlt mir nach wie vor eine überzeugende Erklärung. Oder eben: eine Quelle.
Viele Grüße
Holger Handstein
Natürlich ist die Spanne -0,5 bis 0,5 willkürlich, ich habe nie etwas anderes behauptet. Man könnte auch sagen -0,6 bis 0,6 oder -0,65 bis 0,65. Darauf kommt es mir hier nicht an. Sondern darauf, klar zu machen, dass beide Exteme schlecht sind: Zu hohe positive Korrelation, genauso wie zu hohe negative Korrelation. Das eine erhöht das Risiko über die Maßen ohne dass eine signifikante Erhöhung der Zielrendite zu erwarten ist. Das andere reduziert signifkant das Risiko bei gleichzeitiger signifikanten Reduktion der Zielrendite.
Wir können natürlich versuchen, sehr kompliziert, Leute zu informieren. Zielführender ist es jedoch, eine leicht verständliche Sprache zu verwenden und den Leuten eine Maxime an die Hand zu geben, mit der sie schnell die richtige Entscheidung treffen können. Die Maxime „Eine möglichst negative Korrelation“ kann mitunter – in großen Ausnahmefällen – zu einer richtigen Anlageentscheidung führen, in der Regel aber, wird durch diese Maxime der Anleger fehlgeleitet. Das ist der entscheidende Punkt.
Daher ist es besser, gleich klipp und klar zu sagen: „Eine Korrelation von um die Null ist erstrebenswert“. Das stimmt zwar nicht in 100%ig allen Fällen, aber fast immer. Und durch solch eine Maxime helfen wir den normalen Anlegern mehr als durch die andere Maxime, die in der Praxis sehr häufig zu gravierenden Fehlentscheidungen führen wird. Wie gesagt, ich hatte schon ein paar Mal asugesprochen stolze Anleger bei mir, die ein long-Produkt mit einem direkten short-Produkt kombiniert hatten und glauben so für eine optimale Diversifikation gesorgt zu haben. Genau nach dem vermeintlichen Maxime „Je negativer die Korrelation, je besser!“ – Genau diese Anleger wunderten sich aber über ihre schlechte Performance. Und wenn ich ihnen sagte: „Naja, die schlechte Performance liegt an der fast perfekten Korrelation Ihrer Anlageprodukte“, dan bekam ich solche Antworten wie „Aber warum? Je negativer die Korrealtion ist, um so besser ist doch die Diversifikation.“ Ja, das stimmt, das Risiko geht runter, aber eben auch die Zielrendite! Und man erhält so ein Portfolio, das der Anleger ursprünglich eigentlich gar nicht wollte.
„Und wenn ich ihnen sagte: ‚Naja, die schlechte Performance liegt an der fast perfekten Korrelation Ihrer Anlageprodukte'“
Lieber Dr. Peterreins. Es tut mir wirklich leid, dass ich Ihnen da so hartnäckig widersprechen muss, aber diese Aussage ist so einfach nicht richtig. Richtig wäre:
Es liegt daran, dass in diesem Fall der Erwartungswert der Rendite von Asset A dem negativen Erwartungswert von Asset A entspricht (plus Geldmarktzinsen, minus Kosten).
Also: Erwartungsrendite A = Erwartungsrendite * -1
Das ist zwar nur bei einer perfekt gegenläufigen Korrelation möglich – es ist aber nicht so, dass ein KK von -1 eine hinreichende Bedingung dafür wäre. Noch einmal die beiden zusätzlichen Stichworte (auf die Sie bisher nicht eingegangen sind):
– Erwartungwert
– Volatilität
Wer auf die haarsträubende Idee kommt, dass es eine sinnvolle Anlagestrategie sein könnte, einen Long- und einen Short-ETF auf den gleichen Index zu kombinieren, der benötigt in der Tat einen guten Anlageberater. Aber das hat nichts damit zu tun, dass eine negative Korrelation zweier Assets nicht erstrebenswert wäre.
Lieber Herr Handstein,
wenn zu mir jemand kommt und sagt, er hätte ein Wertpapier gefunden, das mit 100%iger Sicherheit 7% Rendite bringt, dann würde ich sofort sagen: „Tut mir leid, das glaube ich nicht.“ Jetzt kann man natürlich argumentieren, dass es prinzipiell nicht ausgeschlossen ist, dass es ein solches Wertpapier gibt. Aber bei Tagesgeldzinsen von etwa 2% p.a. würde ich ein solche Wertpapeir für extrem unwahrscheinlich halten. Daher gebe ich ohne zu zögern die Devise an Anleger aus: „Finger weg von Anlageformen, die eine hohe Rendite in Aussicht stellen und gleichzeitig Null Risiko versprechen. Irgendwo wird da ein Haken sein.“ Auch hier könnte man mir vorwerfen, dass ich zu pauschal spreche, und dass es doch denkbar sein, einmal eine solche Anlageform irgendwie zu finden.
Und tatsächlich suchen ja einige Anleger genau nach solchen Investments: Hohe Renditen mit Null Risiko. Und hin und wieder glaubt tatsächlich ein Anleger, so etwas gefunden zu haben. Vor vielen Jahren beispielsweise gab es so eine Welle, wo alle möglichen Anleger zu mir gekommen sind und sich damit gebrüstet haben, dass sie ganz lukrative Swap-Geschäfte abgeschlossen hätten. Ich warnte diese Anleger und sagte, da schlummerten enorme Risiken. Eine bemerkenswert große Anzahl dieser Anleger glaubte mir nicht, sie hielten Swap-Geschäfte für eine risikofreie Gelddruckmaschine. Heute sind sie klüger, weil sie die Sache jedes Mal mit gigantischen Verlusten endete.
Als Beispiel könnte ich auch offene Immobilienfonds nehmen. Auch hier meinten Anleger für lange Zeit, dass man hier mehr Rendite erhalten könnte als mit Tagesgeld möglich ist, aber bei gleicher Sicherheit. Das war natürlich auch eine Illusion, wie man heute weiß.
Und genau dieselbe Analogie gibt es mit bezug auf negative Korrelationen. Nehmen wir folgende Situation an. Ein Anleger kommt zu mir und sagt:
„Ich habe seit langem ein Wertpapier A. Ich überlege mir ob ich entweder das Werpapier X oder das Wertpapier Y aus Diversifikationsgründen dazukaufe. Beim Wertpapier X habe ich für die letzten drei Jahre eine Korrelation von -0,4 ausgerechnet, für das Wertpapier Y eine Korrelation von -0,95. Herr Peterreins, welches dieser beiden Wertpapiere, raten Sie mir zu erwerben?“
Und nehmen wir an, dass ich außer diesen Korrelationen überhaupt nichts über diese Wertpapiere wüsste. Ich würde dem Anleger ohne zu zögern, das Wertpapier X (mit der Korrelation -0,4) raten, und ihm von Y (mit der Korrelation -0,95) abraten. Ganz genauso wie ich jemanden vor einem Wertpapier warnen würde, von dem behauptet wird: Hohe Rendite plus Null Risiko.
Natürlich ist es prinzipiell denkbar, dass die gemeinsame zu erwartende Rendite von A und Y größer als Tagesgeld ist. Das ist aber in etwa so unwahrscheinlich wie ein völlig risikofreies Wertpapier zu finden, das eine Zielrendite von 7% verspricht. Beides würde ich zunächst anzweifeln. Und so wie ich als Handlungsmaxime sage: „Passt gut auf bei Anlageformen, bei denen euch hohe Renditen mit Null Risiko versprochen werden! Irgendwo wird es einen Haken geben“, so gebe ich die Handlungsmaxime aus: „Passt extrem gut auf bei Korrelationen von sagen wir -0,9 und -1,0! Irgendwo wird es einen Hagen geben!“
Mir ist jedenfalls klar, dass es keinesfalls gut ist zu sagen: „Je näher die Korrelation bei -1 ist, umso besser.“ Diese Maxime verführt sicherlich zu Fehlentscheidungen. Und ja, möglicherweise findet ja mal jemand zwei so unwahrscheinliche Werptpapiere, die perfekt negativ korreliert sind und deren gemeinsame Rendite deutlich über Tagesgeld liegt. Genauso wie ich nicht prinzipiell ausschließen kann, dass jemand mal eine Anlageform finden wird, mit der man ohne jegliches Risiko 7% p.a. erzielen kann. Man kann ja mal auf die Suche gehen. Aber die Wahrscheinlichkeit, etwas zu finden ist sehr, sehr gering.
Sorry, in der kleinen Gleichung fehlte natürlich ein Buchstabe. Richtig ist:
Erwartungsrendite A = Erwartungsrendite B * -1
Dennoch, wirft sich mir eine Frage auf:
In diesem Beitrag wird nur Bezug auf die Renditemöglichkeit in Form von Kurssteigerungen aber nicht die der Dividendenausschüttung berücksichtigt;
Wenn ich mir zwei perfekt negativ korrelierte Wertpapiere aneigne, habe ich keine Rendite mehr in Form vom Kursgewinn, dennoch erhalte ich eine Dividende, abgesehen vom ETF.
Mich würde daher wie sich meine Rendite verhält, wenn ich in zwei perfekt negativ korrelierte Aktien investiere, somit das diversifizierbare Risiko minimiere, dafür keinen Kursgewinn mitnehme, aber dennoch die Dividende beider Unternehmensbeteiligungen erhalte.
Ich habe zwar nur von Kurssteigerungen geredet, habe aber immer gemeint: Kursveränderungen + Dividendenausschüttungen.
Wenn man zwei perfekt negativ korrelierte Aktien A und B erwirbt, so MUSS auch mit Berücksichtigung etwaiger Dividendenausschüttungen die Gesamtrendite (A+B) entweder bei der Geldmarktrendite liegen oder leicht darunter. Es ist ja auch so, dass eine Aktie normalerweise entsprechend der ausgeschütteten Dividende fällt am Tage der Ausschüttung. Also nehmen wir an, dass eine Aktie heute 100 € wert ist, morgen 2 € ausschüttet, dann müsste der Kurs morgen normalerweise bei 98 liegen. Liegt er hingegen nach wie vor bei 100 €, naja, dann hat die Aktie an diesem Tag eigentlich noch einen Kursgewinn von 2 € hingelegt.
Ein Depot mit Long und Short Position auf den DAX bringt zwar in der Summe einen Ertrag von Null (ohne Berücksichtigung von Transaktionskosten), man könnte aber auch argumentieren, dass in Zeiten von Negativzinsen dies eine gute Anlage sei.
Was bei einer Short/Long- Kombination vergessen wird: Bei der Shortposition hole ich mir ein Kontrahenten-Risiko mit ins Depot. Oder im Sinne der Kapitalmarkttheorie ein unsystematisches Risiko – also gerade kein „free lunch“ – weil SWAP/Futures/Optionen verpackt in ETFs weiter SWAP/Futures/Optionen bleiben.